[Course] Coarse geometry and operator algebras: a minicourse
Sep. 19, 2022
Speaker: Yeong Chyuan Chung, Leiden University
Time: 19:30-20:30, September 19-22/26-29, 2022, GMT+8
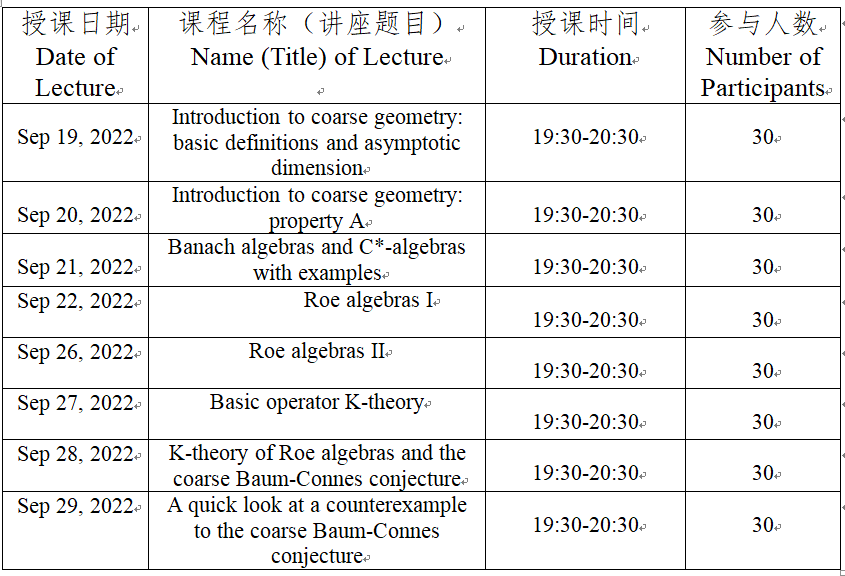
Timetable:
Venue: Tecent Meeting ID: 869-2118-6000 Password: 3721
Abstract:
Coarse geometry involves studying metric spaces by looking at them from far away, and it is important in areas of mathematics such as geometric group theory. In recent times, its interaction with operator algebras has also been an active area of research with applications to problems in topology and differential geometry. In this mini-course, we aim to introduce basic notions in coarse geometry and a class of operator algebras known as Roe algebras. Starting from coarse geometry, we will introduce basic definitions such as coarse embeddings and coarse equivalences, then we will introduce some coarse geometric invariants such as asymptotic dimension and property A. Next, we will introduce Banach algebras and C*-algebras with examples of these, then we will focus on Roe algebras and how they reflect the coarse geometry of the underlying metric spaces. Finally, we will briefly introduce operator K-theory and the coarse Baum-Connes conjecture involving the K-theory of Roe algebras.
Biography:
Yeong Chyuan Chung, obtained his Ph.D. from Texas A&M University in 2017, mainly engaged in the research of rough geometry, L^p operator algebra, K-theory. In recent years, he has published many high-level papers in J. Funct. Anal., J. Noncommut. Geom. and other journals.
Source: SRMC